Tabla de Funciones Trigonométricas

Para el cálculo del valor de las funciones trigonométricas se confeccionaron tablas trigonométricas. La primera de estas tablas fue desarrollada por Johann Müller Regiomontano en 1467, que nos permiten, conocido un ángulo, calcular los valores de sus funciones trigonométricas. En la actualidad dado el desarrollo de la informática, en prácticamente todos los lenguajes de programación existen librerías de funciones que realizan estos cálculos, incorporadas incluso en calculadoras electrónicas de bolsillo, por lo que el empleo actual de las tablas resulta obsoleto.

Razones Trigonométricas

 

Descarga el Archivo en .pdf

Series  razones  trigonometricas 

Ecuación de Segundo Grado

 

Clicka aquí para descargar el archivo completo

Suma y Resta de Fracciones con Diferente Denominador

La Circunferencia Y La Recta

Circunferencia: Es una curva plana y cerrada cuyos puntos equidistan de un punto interior llamado centro. Círculo: Es la duperficie limitada por al circunferencia.   Diámetro: Es una cuerda que pasa por el centro de la circunferencia. Cuerda: Es un segmento que une dos puntpos cualesquiera de la circunferencia sin pasar por el centro.
Radio: Es un segmento que une al centro con cualquier punto de la circunferencia. Arco: Es el segmento curvilíneo de puntos pertenecientes a la circunferencia de radio máximo.

 

 

Secante: Es una recta que corta a una circunferencia en 2 puntos. Conforme estos puntos se acercan y su distancia se reduce a cero, la recta adquiere el nombre de recta Tangente.

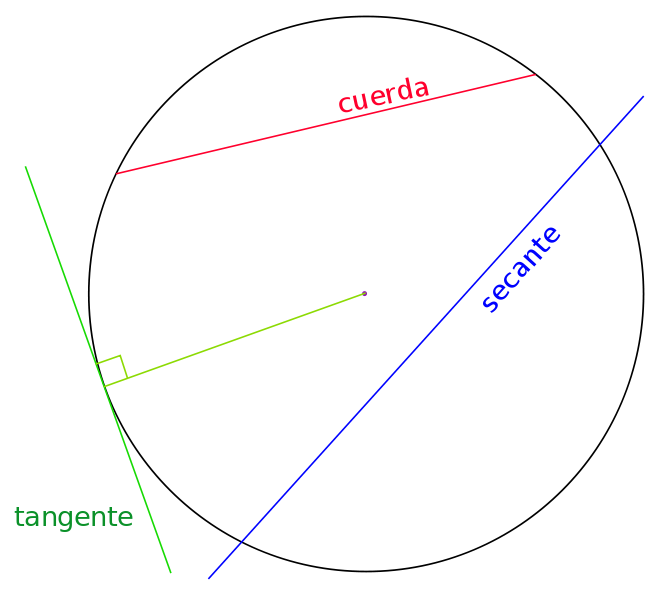
Tangente

En geometría, una recta tangente es aquella que solo tiene un punto en común con una curva, es decir la toca en un solo punto, que se llama punto de tangencia. La recta tangente indica la pendiente de la curva en el punto de tangencia.

En trigonometría, la tangente de un ángulo es la relación entre los catetos de un triángulo rectángulo: es el valor numérico resultante de dividir la longitud del cateto opuesto entre la del cateto adyacente a dicho ángulo.

 

Congruencia entre Triángulos

Podemos afirmar que los triángulos congruentes tienen la misma forma y tamaño; podemos señalar que los criterios de congruencia entre triángulos son:

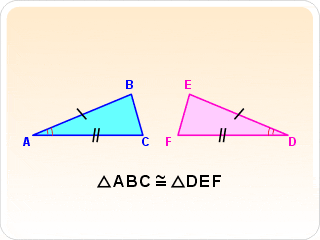
2 Triángulos son congruentes (iguales) si tienen respectivamente iguales 2 lados y el ángulo comprendido entre ellos.

 LAL= Lado - Ángulo - Lado

 Serán congruentes (iguales) aquellos triángulos que tienen respectivamente iguales los lados que los forman

LLL = Lado -  Lado -  Lado

  ALA = Ángulo Lado - Ángulo  

Cómo dibujar Triángulos

 

Cálculo de elementos en un triángulo rectángulo

Factorización Y Productos Notables

Una Ecaución Cuadrática es la que tiene variables elevados al cuadrado, es decir, a la segunda potencia.

Los productos Notables y la Factorización son formas abreviadas de realizar multipilicaciones de binomios. 

Factorizar un polinomio cuyos términos tienen un factor común. 

Sabemos que  m( x - y + z ) = mx - my + mz. Luego, factorizar este último polinomio es simplemente proceder a la inversa, buscando el factor común. O sea mx - my + mz = m( x - y + z ).

 

Factorizar un trinomio cuadrado perfecto. Sabemos que (a±

b)² = a² ± 2ab + b². Luego, se tendrá inversamente que a² ± 2ab + b²=(a ± b)².

Factorización de la diferencia de dos cuadrados. Sabemos que (a + b)(a - b) = a² - b². Luego, se tendrá inversamente que: a² - b² = (a + b)(a - b).

Factorizar un trinomio de la forma  x² + mx + n. Sabemos que (x + a)(x + b) = x² + (a + b)x + ab. Luego, se tendrá inversamente que: x² + (a + b)x + ab = (x + a)(x + b)

Ejemplo de Multiplicación de Binomios:

m+3

m+3

m²+3m

+3m+9

 m ² +6m+9

Al multiplicar binomios tenemos que realizar la multiplicación de todos los términos que se suman por los términos del toro binomio. Al final, sumamos términos semejantes (Contienen variables elevadas a la misma potencia)

 Ejémplo Gráfico en un Cuadrado:

Ejemplo en video:

Variables en una Ecuación

En una operación Matemática podemos encotnrar ciertas incógnitas cuyo valor desconocemos. Dichas incógnitas se conocen como variables.

2x+1= 3

¿ Puedes adivinar que valor hace cierta a esta expresión?

R=1

Una expresión matemática con variables es conocida como ecuación cuando tiene un resultado, es decir, cuando usa el signo de "igual = ", y habrá un sólo resultado correcto que hará verdadera a la ecuación.

Ese resutado es justamente el valor de la variable. Sin embargo la forma común de encontrar una variable que haga cierta a una ecuación no es "adivinandola". La forma matemática que mas se emplea en estos casos son los Despejes

En general podemos decir que despejar significa manipular una ecuación siguiendo las reglas de las operaciones matemáticas, para obtener otra ecuación en donde la variable a despejar se encuentre sola de un lado de la ecuación.

Ejemplo: 1.- Si hacemos las misma operacion sobre los dos lados de una igualdad, esta sigue siendo válida:

2x+1-1 = 3-1

2x/2 = 2/2

x = 1

2.- Toda operación matemática tiene su inversa a realizar operaciones inversas es como "respetar" la ecuación, siempre que se apliquen en ambos lados de la igualdad.

3.- Para despejar una ecuación hay que respetar el orden de operaciones, es decir, al despejar debemos hacer las operaciones inversas, respetando su órden jerárquico:

b = 2 + 1

      2a

2b= (2+1) / a=X

2b=2+1

a

2ba=2+1

2ba=3

a=3

    2b