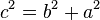Uso de la Tabla de Logaritmos.
Para poder calcular con la tabla de logaritmos debemos tener en cuenta lo siguiente.-
Un logaritmo cuenta con dos partes:
- a) Característica = que es la parte entera de una cifra.
- b) Mantiza = que es la parte decimal de una cifra.
Forma de calcular a través de la tabla de logaritmos.
1.- Paso:
Se debe contar los dígitos de la parte entera de la cifra y al total restarle 1.
Ejem:
Log 85975 = Tiene 5 dígitos por lo tanto seria = 4,
Log 245,75 = Tiene 3 dígitos por lo tanto seria = 2,
2.- Paso:
Se debe tomar los 2 primeros dígitos de la cifra los cuales indicarían la fila a la que pertenece.
Ejem:
Log 85975 = El par seria = Fila 85.
Log 245,75 = El par seria = Fila 24.
3.- Paso:
Se debe tomar el 3er digito de la cifra el cual indicara la columna a la cual pertenece.
Ejem:
Log 85975 = Esto seria = Columna 9.
Log 245,75 = Esto seria = Columna 5.
Resumen:
Log 857 = tiene 3 dígitos entonces quedarían 2, pertenece a la fila 85, columna 7 y seria igual a: "Log 2,9330".
| Número | Logaritmo | Logaritmo neperiano |
| 1 | 0,000000 | 0,000000 |
| 2 | 0,301030 | 0,693147 |
| 3 | 0,477121 | 1,098612 |
| 4 | 0,602060 | 1,386294 |
| 5 | 0,698970 | 1,609438 |
| 6 | 0,778151 | 1,791759 |
| 7 | 0,845098 | 1,945910 |
| 8 | 0,903090 | 2,079442 |
| 9 | 0,954243 | 2,197225 |
| 10 | 1,000000 | 2,302585 |
| 11 | 1,041393 | 2,397895 |
| 12 | 1,079181 | 2,484907 |
| 13 | 1,113943 | 2,564949 |
| 14 | 1,146128 | 2,639057 |
| 15 | 1,176091 | 2,708050 |
| 16 | 1,204120 | 2,772589 |
| 17 | 1,230449 | 2,833213 |
| 18 | 1,255273 | 2,890372 |
| 19 | 1,278754 | 2,944439 |
| 20 | 1,301030 | 2,995732 |
| 21 | 1,322219 | 3,044522 |
| 22 | 1,342423 | 3,091042 |
| 23 | 1,361728 | 3,135494 |
| 24 | 1,380211 | 3,178054 |
| 25 | 1,397940 | 3,218876 |
| 26 | 1,414973 | 3,258097 |
| 27 | 1,431364 | 3,295837 |
| 28 | 1,447158 | 3,332205 |
| 29 | 1,462398 | 3,367296 |
| 30 | 1,477121 | 3,401197 |
| 31 | 1,491362 | 3,433987 |
| 32 | 1,505150 | 3,465736 |
| 33 | 1,518514 | 3,496508 |
| 34 | 1,531479 | 3,526361 |
| 35 | 1,544068 | 3,555348 |
| 36 | 1,556303 | 3,583519 |
| 37 | 1,568202 | 3,610918 |
| 38 | 1,579784 | 3,637586 |
| 39 | 1,591065 | 3,663562 |
| 40 | 1,602060 | 3,688879 |
| 41 | 1,612784 | 3,713572 |
| 42 | 1,623249 | 3,737670 |
| 43 | 1,633468 | 3,761200 |
| 44 | 1,643453 | 3,784190 |
| 45 | 1,653213 | 3,806662 |
| 46 | 1,662758 | 3,828641 |
| 47 | 1,672098 | 3,850148 |
| 48 | 1,681241 | 3,871201 |
| 49 | 1,690196 | 3,891820 |
| 50 | 1,698970 | 3,912023 |
| 51 | 1,707570 | 3,931826 |
| 52 | 1,716003 | 3,951244 |
| 53 | 1,724276 | 3,970292 |
| 54 | 1,732394 | 3,988984 |
| 55 | 1,740363 | 4,007333 |
| 56 | 1,748188 | 4,025352 |
| 57 | 1,755875 | 4,043051 |
| 58 | 1,763428 | 4,060443 |
| 59 | 1,770852 | 4,077537 |
| 60 | 1,778151 | 4,094345 |
| 61 | 1,785330 | 4,110874 |
| 62 | 1,792392 | 4,127134 |
| 63 | 1,799341 | 4,143135 |
| 64 | 1,806180 | 4,158883 |
| 65 | 1,812913 | 4,174387 |
| 66 | 1,819544 | 4,189655 |
| 67 | 1,826075 | 4,204693 |
| 68 | 1,832509 | 4,219508 |
| 69 | 1,838849 | 4,234107 |
| 70 | 1,845098 | 4,248495 |
| 71 | 1,851258 | 4,262680 |
| 72 | 1,857332 | 4,276666 |
| 73 | 1,863323 | 4,290459 |
| 74 | 1,869232 | 4,304065 |
| 75 | 1,875061 | 4,317488 |
| 76 | 1,880814 | 4,330733 |
| 77 | 1,886491 | 4,343805 |
| 78 | 1,892095 | 4,356709 |
| 79 | 1,897627 | 4,369448 |
| 80 | 1,903090 | 4,382027 |
| 81 | 1,908485 | 4,394449 |
| 82 | 1,913814 | 4,406719 |
| 83 | 1,919078 | 4,418841 |
| 84 | 1,924279 | 4,430817 |
| 85 | 1,929419 | 4,442651 |
| 86 | 1,934498 | 4,454347 |
| 87 | 1,939519 | 4,465908 |
| 88 | 1,944483 | 4,477337 |
| 89 | 1,949390 | 4,488636 |
| 90 | 1,954243 | 4,499810 |
| 91 | 1,959041 | 4,510860 |
| 92 | 1,963788 | 4,521789 |
| 93 | 1,968483 | 4,532599 |
| 94 | 1,973128 | 4,543295 |
| 95 | 1,977724 | 4,553877 |
| 96 | 1,982271 | 4,564348 |
| 97 | 1,986772 | 4,574711 |
| 98 | 1,991226 | 4,584967 |
| 99 | 1,995635 | 4,595120 |
| 100 | 2,000000 | 4,605170 |


![]0,+\infty[](http://upload.wikimedia.org/math/e/b/8/eb8a0ceeec2805d7e3ba7c0591eafa52.png)
![]-\infty,+\infty[](http://upload.wikimedia.org/math/d/a/6/da6b9b99f9b93ed32a0cc8706361afa7.png)




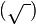


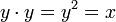
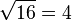















 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que: